Kunci Jawaban Matematika Kelas 9 Halaman 303, 304, 305, Menghitung Bola

TRIBUNKALTIM.CO -  Cek referensi kunci jawaban Matematika kelas 9 halaman 303 hingga 305 berikut tentang menghitung bola.

Diharapkan siswa Kelas 9 SMP sebelum melihat kunci jawaban Matematika kelas 9 halaman 303 , 304, 305 untuk memahami materi bola untuk menjawab 10 soal yang tersedia.

Tidak menutup kemungkinan pada kunci jawaban Matematika kelas 9 halaman 303 hingga 305 berikut terdapat kesalahan penghitungan.

Pada 10 soal berikut tentang menghitung bola terdapat di dalam materi Matematika Kelas 9 SMP Bab 5 Bangun Ruang Sisi Lengkung.

Di Bab 5 Bangun Ruang Sisi Lengkung ini, siswa Kelas 9 SMP tak hanya mempelajari menghitung bola, melainkan juga kerucut dan tabung.

Baca juga: Contoh Soal dan Kunci Jawaban UTS atau PTS Matematika Kelas 9 SMP Semester 2 Pilihan Ganda

Siswa Kelas 9 SMP usai mempelajari materi ini diharapkan mampu:

1. Mengenali bangun tabung, kerucut dan bola beserta unsur-unsurnya

2. Menentukan jaring-jaring tabung, kerucut dan bola

3. Mengidentifikasi luas permukaan tabung, kerucut dan bola

4. Menentukan hubungan antara luas alas dan tinggi dengan volume

5. Mengidentifikasi volume tabung, kerucut dan bola

6. Menyelesaikan permasalahan nyata

Simak berikut referensi kunci jawaban Matematika kelas 9 halaman 303 hingga 305 yang dikutip dari Tribunnews.

Latihan 5.3

Bola

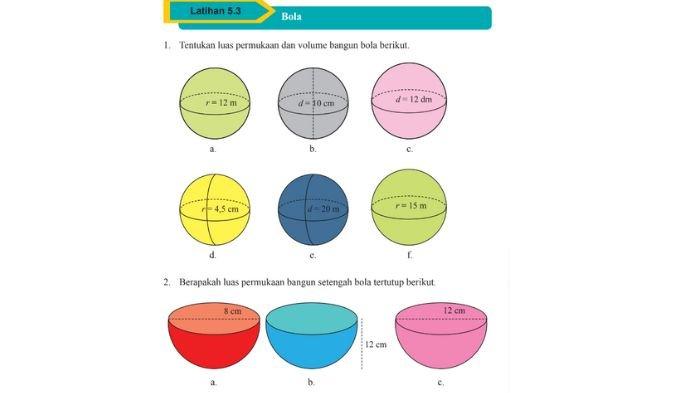
1. Tentukan luas permukaan dan volume bangun bola berikut.

Jawaban:

Gunakan rumus luas permukaan dan volume bola. Jika diketahui diameter ubah menjadi jari-jari.

Volume bola = 4/3 x π × r3
Luas permukaan bola = 4 × π × r2

a) Luas = 4 x π x 12 x 12
= 576π m2

Volume = 4/3 x π x 12 x 12 x 12
= 2304π m3

b) Luas = 4 x π x 5 x 5
= 100π cm2

Volume = 4/3 x π x 5 x 5 x 5
= 500/3π cm3

c) Luas = 4 x π x 6 x 6
= 144π dm2

Volume = 4/3 x π x 6 x 6 x 6
= 288π dm3

d) Luas = 4 x π x 4,5 x 4,5
= 81π cm2

Volume = 4/3 x π x 4,5 x 4,5 x 4,5
= 243/2π cm3

e) Luas = 4 x π x 10 x 10
= 400π m2

Volume = 4/3 x π x 10 x 10 x 10
= 4000/3π m3

f) Luas = 4 x π x 15 x 15
= 900π m2

Volume = 4/3 x π x 15 x 15 x 15
= 4500π m3

Baca juga: Kunci Jawaban Matematika Kelas 8 Semester 2 Halaman 144, 145, 146, 147, Menghitung Prisma

2. Berapakah luas permukaan bangun setengah bola tertutup berikut

Jawaban:

Volume setengah bola = (4/3 x π × r3) / 2
Luas permukaan setengah bola = (4 × π × r2) / 2 + (π × r2)

a) Luas = 48π cm2
Volume = 128/3π cm3

b) Luas = 432π cm2
Volume = 1.152π cm3

c) Luas = 108π cm2
Volume = 144π cm3

d) Luas = 192π m2
Volume = 1.024/3π m3

e) Luas = 675/4π m2
Volume = 1.125/4π m3

f) Luas = 363π dm2
Volume = 2.662/3π dm3

3. Dari soal-soal nomor 2 tentukan rumus untuk menghitung luas permukaan setengah bola tertutup.

Jawaban:

Luas permukaan stengah bola = 1/2 luas permukaan bola + luas lingkaran
= 1/2 4πr2 + πr2
= 3πr2

4. Tentukan jari-jari dari bola dan setengah bola tertutup berikut.

Jawaban:

a) L = 4 × π × r2
729π = 4 x π x r2
r = √(729/4)
r = 27/2 cm

b) V = 4/3 x π × r3
2.304π = 4/3 x π x r3
r3 = 2.304 x 3/4
r = 12 cm

c) V = 4/3 x π × r3
36π = 4/3 x π x r3
r3 = 36 x 3/4
r = 3 cm

d) L = 3 × π × r2
27π = 4 x π x r2
r = √(27/3
r = 3 m

e) L = 3 × π × r2
45π = 3 x π x r2
r = √(45/3
r = √15 m

f) V = 2/3 x π × r3
128/3π = 2/3 x π x r3
r3 = 128/3 x 3/2
r = 4 m

Baca juga: Kunci Jawaban Matematika Kelas 8 Halaman 113, 114, 115, 116 Semester 2, Menghitung Lingkaran

5. Berpikir kritis.Terdapat suatu bola dengan jari-jari r cm. Jika luas permukaan bola tersebut adalah A cm2 dan volume bola tersebut adalah A cm3, tentukan:

a. nilai r
b. nilai A

Jawaban:

a) Luas permukaan = 4πr2
Volume = 4/3 πr3
4πr2= 4/3 πr3
r = 3 cm

b) Luas permukaan = 4πr2
= 4π(3)2
= 36π

6. Bangun di samping dibentuk dari dua setengah bola yang sepusat. Setengah bola yang lebih kecil memiliki jari-jari r1 = 4 cm sedangkan yang lebih besar memiliki jari-jari r2 = 8 cm.

Tentukan:

a. luas permukaan bangun tersebut,
b. volume bangun tersebut.

Jawaban:

a. Luas permukaan = 1/2 luas permukaan bola besar x 1/2 luas permukaan bola kecil + luas lingkaran besar - luas lingkaran kecil
= ½ . 4π(8)2 + ½ × 4π(4)2 + π(8)2 – π(4)2
= 128π + 32π + 64π – 16π
= 208π cm2

b. Volume = Volume setengah bola besar – volume setengah bola kecil
= 2/3 π(8)3 – 2/3 π(4)3
= 2/3 π(512 – 64)
= 2/3 π × 448
= 896/3 π cm3

7. Analisis kesalahan. Lia menghitung luas permukaan bola dengan cara membagi volume bola dengan jari-jari bola tersebut (L = V/r). Tentukan kesalahan yang dilakukan oleh Lia.

Jawaban:

L = 4πr2, V = 4/3 πr3

Sehingga V = Lr/3, yang berakibat L = 3V/r

8. Bola di dalam kubus. Terdapat suatu kubus dengan panjang sisi s cm. Dalam kubus tersebut terdapat bola dengan kondisi semua sisi kubus menyentuh bola

a. Tentukan luas permukaan bola tersebut.
b. Tentukan volume bola tersebut.

Petunjuk: tentukan jari-jari bola terlebih dahulu.

Jawaban:

Karena semua sisi kubus menyentuh bola maka diameter bola = s, jari-jari bola = s/2

a) Luas permukaan bola = 4 × π × r2
= 4 x π x s/2 x s/2
= πs2 cm2

b) Volume bola = 4/3 x π × r3
= 4/3 x π x s/2 x s/2 x s/2
= πs3/6 cm3

9. Kubus di dalam bola. Terdapat suatu kubus dengan panjang sisi s cm. Kubus tersebut berada di dalam bola dengan kondisi semua titik sudut kubus menyentuh bola.

a. Tentukan luas permukaan bola tersebut
b. Tentukan volume bola tersebut

Petunjuk: tentukan jari-jari bola terlebih dahulu

Jawaban:

Diagonal bidang kubus = diameter bola, diperoleh r = 1/2√3s

a) Luas = 4πr2
= 4π(1/2√3s)2
= 3πs2 cm2

b) Volume = 4/3πr3
= 4/3π(1/2√3s)3
= 1/2√3πs3 cm3

10. Timbangan dan kelereng. Andi punya dua macam kelereng. Kelereng tipe I berjari-jari 2 cm sedangkan tipe II berjari-jari 4 cm. Andi melakukan eksperimen dengan menggunakan timbangan. Timbangan sisi kiri diisi dengan kelereng tipe I sedangkan sisi kanan diisi dengan kelereng tipe II. Tentukan perbandingan banyaknya kelereng pada sisi kiri dengan banyaknya kelereng pada sisi kanan agar timbangan tersebut seimbang

Jawaban:

Misalkan banyaknya kelereng tipe I adalah m sedangkan tipe II adalah n.

V1 = 4/3π(2)3 = 32/3π cm
V2 = 4/3π(4)3 = 256/3π cm

m x V1 = n x V2π
m x 32/3π = n x 256/3π
m = 8n

Sehingga, perbandingan banyak kelereng pada sisi kiri dengan sisi kanan agar seimbang adalah 8 : 1.

*) Disclaimer:

- Artikel ini hanya ditujukan kepada orang tua untuk memandu proses belajar anak.

- Sebelum melihat kunci jawaban, siswa harus terlebih dahulu menjawabnya sendiri, setelah itu gunakan artikel ini untuk mengoreksi hasil pekerjaan siswa.

(*)

BERITA PENDIDIKAN

BERITA BEASISWA