Kunci Jawaban Matematika Kelas 8 Semester 2 Halaman 308 hingga 310, 10 Soal Esai Tentang Peluang

TRIBUNKALTIM.CO - Berikut referensi kunci jawaban Matematika kelas 8 halaman 308 hingga 310 yang bisa dijadikan bahan evaluasi belajar siswa tentang peluang.

Soal Matematika kelas 8 SMP ini berisikan 10 esai tentang materi peluang.

Meskipun telah tersedia kunci jawaban Matematika kelas 8 halaman 308 hingga 310, siswa kelas 8 SMP diharapkan mempelajari lebih dulu materi tersebut.

Bimbingan orang tua tentu diperlukan dalam menjawab soal Matematika kelas 8 SMP berikut ini.

Baca juga: Kunci Jawaban Matematika Kelas 8 Semester 2 Halaman 305 306 307, Pilihan Ganda Tentang Peluang

Siswa kelas 8 SMP usai mempelajari materi peluang diharapkan mampu:

1. Melakukan suatu percobaan untuk menentukan peluang empirik.

2. Menentukan ruang sampel dari suatu eksperimen.

3. Menentukan titik sampel yang memenuhi suatu kejadian.

4. Menganalisis keterkaitan antara peluang empirik dengan peluang teoretik.

Berikut kunci jawaban Matematika kelas 8 halaman 308 hingga 310 semester 2 yang dikutip dari Tribunnews.

B. Esai

1. Dari 10 kali pelemparan mata uang logam, diperoleh 4 kali muncul gambar.

a. Tentukan peluang empirik muncul gambar.

b. Tentukan peluang empirik muncul angka.

Jawaban:

a. n = 4
s = 10

P(gambar) = n / s
P(gambar) = 4 / 10
P(gambar) = 2/5

Jadi, peluang empirik muncul gambar adalah 2/5.

b. n = 10 - 4 = 6
s = 10

P(angka) = n / s
P(angka) = 6 / 10
P(angka) = 3/5

Jadi, peluang empirik muncul angka adalah 3/5.

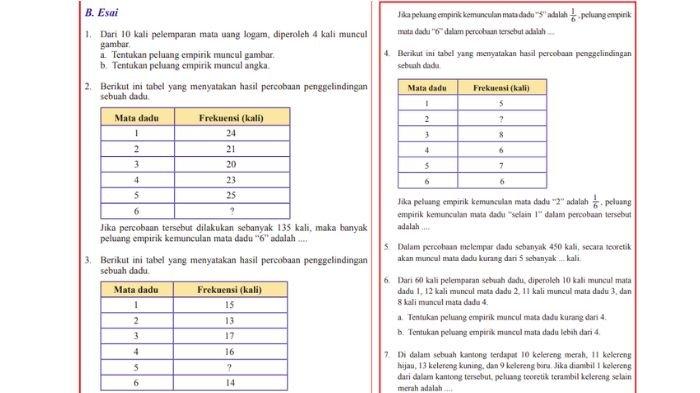
2. Berikut ini tabel yang menyatakan hasil percobaan penggelindingan sebuah dadu. (pada buku)

Jika percobaan tersebut dilakukan sebanyak 135 kali, maka banyak peluang empirik kemunculan mata dadu “6” adalah ....

Jawaban:

s = 135
24 + 21 + 20 + 23 + 25 + x = 135
113 + x = 135
x = 135 - 113
x = 22

P = n / s
P = 22/135

Jadi, peluang empirik kemunculan mata dadu 6 adalah 22/135.

3. Berikut ini tabel yang menyatakan hasil percobaan penggelindingan sebuah dadu. (pada buku)

Jika peluang empirik kemunculan mata dadu “5” adalah 1/6, peluang empirik mata dadu “6” dalam percobaan tersebut adalah ....

Jawaban:

P(dadu "5") = n / s
1/6 = x / (15 + 13 + 17 + 16 + 14 + x)
1/6 = x / (75 + x)
x = (75 + x) / 6
6x = 75 + x
5x = 75
x = 15

s = (15 + 13 + 17 + 16 + 14 + x)
s = (15 + 13 + 17 + 16 + 14 + 15)
s = 90

P(dadu "6") = n / s
P(dadu "6") = 14 / 90
P(dadu "6") = 7/45

Jadi, peluang empirik mata dadu "6" dalam percobaan tersebut adalah 7/45.

4. Berikut ini tabel yang menyatakan hasil percobaan penggelindingan sebuah dadu. (pada buku)

Jika peluang empirik kemunculan mata dadu “2” adalah 1/6, peluang empirik kemunculan mata dadu “selain 1” dalam percobaan tersebut adalah ....

Jawaban:

Catatan: Seharusnya, peluang empirik kemunculan mata dadu "2" yang benar adalah 1/5 bukan 1/6. Karena jika menggunakan 1/6 maka ruang sampelnya akan bernilai desimal.

P(dadu "2") = n / s
1/5 = x / (5 + x + 8 + 6 + 7 + 6)
1/5 = x / (32 + x)
x = (32 + x) / 5
5x = 32 + x
4x = 32
x = 8

s = (5 + x + 8 + 6 + 7 + 6)
s = (5 + 8 + 8 + 6 + 7 + 6)
s = 40

P(dadu selain "1") = n / s
P(dadu selain "1") = (8 + 8 + 6 + 7 + 6)/ 40
P(dadu selain "1") = 35/40
P(dadu selain "1") = 7/8

Jadi, peluang empirik mata dadu selain "1" dalam percobaan tersebut adalah 7/8.

Baca juga: Kunci Jawaban Matematika Kelas 8 Semester 2 Halaman 263, 264, 265, 266: Hitung Median, Mean, Modus

5. Dalam percobaan melempar dadu sebanyak 450 kali, secara teoretik akan muncul mata dadu kurang dari 5 sebanyak ... kali.

Jawaban:

x = mata dadu kurang dari 5
x = 1,2,3,4
n(x) = 4

P(x) = n / s
P(x) = 4/6
P(x) = 2/3

Fh(x) = P(x) x Banyak percobaan
Fh(x) = 2/3 x 450
Fh(x) = 900/3
Fh(x) = 300 kali

Jadi, secara teoretik akan muncul mata dadu kurang dari 5 sebanyak 300 kali.

6. Dari 60 kali pelemparan sebuah dadu, diperoleh 10 kali muncul mata dadu 1, 12 kali muncul mata dadu 2, 11 kali muncul mata dadu 3, dan 8 kali muncul mata dadu 4.

a. Tentukan peluang empirik muncul mata dadu kurang dari 4.

b. Tentukan peluang empirik muncul mata dadu lebih dari 4.

Jawaban:

a. a = mata dadu kurang dari 4
a = 1,2,3
n(a) = 10 + 12 + 11
= 33

P(a) = n(a) / s(a)
P(a) = 33/60
P(a) = 11/20

Jadi, peluang empirik muncul mata dadu kurang dari 4 adalah 11/20.

b. b = mata dadu lebih dari 4
b = 5,6
b = (60 - 33) - 8
b = 19

P(b) = n(b) / s(b)
P(b) = 19/60

Jadi, peluang empirik muncul mata dadu lebih dari 4 adalah 19/60.

7. Di dalam sebuah kantong terdapat 10 kelereng merah, 11 kelereng hijau, 13 kelereng kuning, dan 9 kelereng biru. Jika diambil 1 kelereng dari dalam kantong tersebut, peluang teoretik terambil kelereng selain merah adalah ....

Jawaban:

a = kelereng selain merah
a = hijau, kuning, biru

n(a) = 11 + 13 + 9
n(a) = 33

s(a) = 10 + 11 + 13 + 9

P(a) = n(a) / s(a)
P(a) = 33/43

Jadi, peluang teoretik terambil kelereng selain merah adalah 33/43.

8. Di dalam sebuah kantong terdapat 15 kelereng merah, 14 kelereng hijau, 13 kelereng kuning, dan n kelereng biru. Jika diambil 1 kelereng dari dalam kantong tersebut, peluang teoretik terambil kelereng biru adalah 8/29. Tentukan peluang teoretik jika yang diambil adalah kelereng hijau.

Jawaban:

b = kelereng biru
n(b) = b

s = merah + hijau + kuning + biru
s = 15 + 14 + 13 + b
s = 42 + b

P(b) = n(b) / s
8/29 = b / (42 + b)
8 x (42 + b) = b x 29
8b + 336 = 29b
21b = 336
b = 336 / 21
b = 16

P(hijau) = n(hijau) / s
= 14 / (15 + 14 + 13 + b)
= 14 / (15 + 14 + 13 + 16)
= 14 / 58
= 7/29

Jadi, peluang teoretik jika yang diambil kelereng hijau adalah 7/29.

9. Suatu lomba sepeda hias diikuti peserta sebanyak:

- 10 orang berumur 6 tahun,

- 24 orang berumur 9 tahun, dan

- 16 orang berumur 10 tahun.

Jika lomba tersebut akan memilih satu orang terbaik, berapa peluang yang akan terpilih adalah peserta berumur 9 tahun?

Jawaban:

n(9tahun) = 24
s = 10 + 24 + 16
s = 50

P(9tahun) = n(9tahun) / s
P(9tahun) = 24 / 50
P(9tahun) = 12/25

Jadi, peluang yang akan terpilih peserta berumur 9 tahun adalah 12/25.

Baca juga: Kunci Jawaban Matematika Kelas 8 Semester 2 Halaman 216, 217, 218, 219, Menghitung Bangun Ruang

10. Ketika berjalan-jalan di sebuah mall, Rudi mendapatkan keberuntungan sebagai pengunjung mall tergpilih di hari itu. Rudi berkesempatan memilih 1 hadiah dari 3 kotak yang sudah disediakan panitia mall. Setiap kotak tersebut berisi bola berwarna merah mewakili mobil, kuning mewakili motor, dan hijau mewakili TV dengan komposisi sebagai berikut. (pada buku)

Rudi hanya diberi kesempatan untuk mengambil 1 hadiah dari salah satu kotak. Tentukan kotak mana yang memiliki peluang terbesar mendapatkan mobil. Jelaskan.

Jawaban:

n(a) = merah = 8
s(a) = 8 + 9 + 10 = 27

P(a) = n(a) / s(a)
P(a) = 8 / 27 x 100 persen
P(a) = 29,6 persen (Peluang Terbesar)

n(b) = merah = 10
s(b) = 10 + 11 + 14 = 35

P(b) = n(b) / s(b)
P(b) = 10 / 35 x 100 persen
P(b) = 28,5 persen

n(c) = merah = 12
s(c) = 12 + 14 + 19 = 45

P(c) = n(c) / s(c)
P(c) = 12 / 45 x 100 persen
P(c) = 26,6 persen

Jadi, kotak yang memiliki peluang terbesar mendapatkan mobil adalah Kotak A.

*) Disclaimer:

- Artikel ini hanya ditujukan kepada orang tua untuk memandu proses belajar anak.

- Sebelum melihat kunci jawaban, siswa harus terlebih dahulu menjawabnya sendiri, setelah itu gunakan artikel ini untuk mengoreksi hasil pekerjaan siswa.

IKUTI BERITA LAINNYA DI GOOGLE NEWS