Buku Tematik
Kunci Jawaban Matematika Kelas 9 Halaman 303, 304, 305, Menghitung Bola
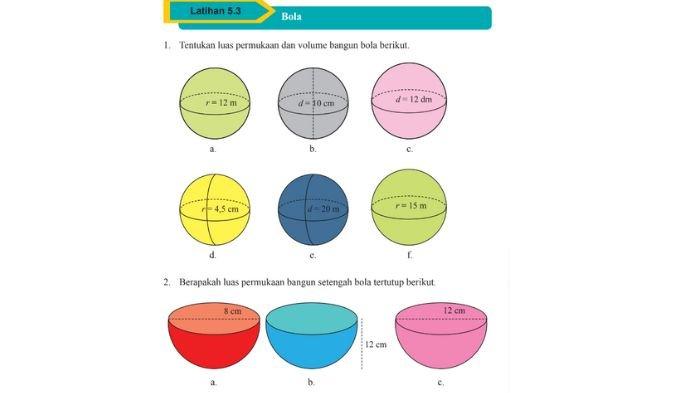
Cek referensi kunci jawaban Matematika kelas 9 halaman 303 hingga 305 berikut tentang menghitung bola.
Penulis: Briandena Silvania Sestiani | Editor: Briandena Silvania Sestiani
a) L = 4 × π × r2
729π = 4 x π x r2
r = √(729/4)
r = 27/2 cm
b) V = 4/3 x π × r3
2.304π = 4/3 x π x r3
r3 = 2.304 x 3/4
r = 12 cm
c) V = 4/3 x π × r3
36π = 4/3 x π x r3
r3 = 36 x 3/4
r = 3 cm
d) L = 3 × π × r2
27π = 4 x π x r2
r = √(27/3
r = 3 m
e) L = 3 × π × r2
45π = 3 x π x r2
r = √(45/3
r = √15 m
f) V = 2/3 x π × r3
128/3π = 2/3 x π x r3
r3 = 128/3 x 3/2
r = 4 m
Baca juga: Kunci Jawaban Matematika Kelas 8 Halaman 113, 114, 115, 116 Semester 2, Menghitung Lingkaran
5. Berpikir kritis.Terdapat suatu bola dengan jari-jari r cm. Jika luas permukaan bola tersebut adalah A cm2 dan volume bola tersebut adalah A cm3, tentukan:
a. nilai r
b. nilai A
Jawaban:
a) Luas permukaan = 4πr2
Volume = 4/3 πr3
4πr2= 4/3 πr3
r = 3 cm
b) Luas permukaan = 4πr2
= 4π(3)2
= 36π
6. Bangun di samping dibentuk dari dua setengah bola yang sepusat. Setengah bola yang lebih kecil memiliki jari-jari r1 = 4 cm sedangkan yang lebih besar memiliki jari-jari r2 = 8 cm.
Tentukan:
a. luas permukaan bangun tersebut,
b. volume bangun tersebut.
Jawaban:
a. Luas permukaan = 1/2 luas permukaan bola besar x 1/2 luas permukaan bola kecil + luas lingkaran besar - luas lingkaran kecil
= ½ . 4π(8)2 + ½ × 4π(4)2 + π(8)2 – π(4)2
= 128π + 32π + 64π – 16π
= 208π cm2
b. Volume = Volume setengah bola besar – volume setengah bola kecil
= 2/3 π(8)3 – 2/3 π(4)3
= 2/3 π(512 – 64)
= 2/3 π × 448
= 896/3 π cm3
7. Analisis kesalahan. Lia menghitung luas permukaan bola dengan cara membagi volume bola dengan jari-jari bola tersebut (L = V/r). Tentukan kesalahan yang dilakukan oleh Lia.
Jawaban:
L = 4πr2, V = 4/3 πr3
Sehingga V = Lr/3, yang berakibat L = 3V/r
8. Bola di dalam kubus. Terdapat suatu kubus dengan panjang sisi s cm. Dalam kubus tersebut terdapat bola dengan kondisi semua sisi kubus menyentuh bola
a. Tentukan luas permukaan bola tersebut.
b. Tentukan volume bola tersebut.
Petunjuk: tentukan jari-jari bola terlebih dahulu.
Jawaban:
Karena semua sisi kubus menyentuh bola maka diameter bola = s, jari-jari bola = s/2
a) Luas permukaan bola = 4 × π × r2
= 4 x π x s/2 x s/2
= πs2 cm2
b) Volume bola = 4/3 x π × r3
= 4/3 x π x s/2 x s/2 x s/2
= πs3/6 cm3
9. Kubus di dalam bola. Terdapat suatu kubus dengan panjang sisi s cm. Kubus tersebut berada di dalam bola dengan kondisi semua titik sudut kubus menyentuh bola.
a. Tentukan luas permukaan bola tersebut
b. Tentukan volume bola tersebut
Petunjuk: tentukan jari-jari bola terlebih dahulu
Jawaban:
Diagonal bidang kubus = diameter bola, diperoleh r = 1/2√3s
a) Luas = 4πr2
= 4π(1/2√3s)2
= 3πs2 cm2
b) Volume = 4/3πr3
= 4/3π(1/2√3s)3
= 1/2√3πs3 cm3
10. Timbangan dan kelereng. Andi punya dua macam kelereng. Kelereng tipe I berjari-jari 2 cm sedangkan tipe II berjari-jari 4 cm. Andi melakukan eksperimen dengan menggunakan timbangan. Timbangan sisi kiri diisi dengan kelereng tipe I sedangkan sisi kanan diisi dengan kelereng tipe II. Tentukan perbandingan banyaknya kelereng pada sisi kiri dengan banyaknya kelereng pada sisi kanan agar timbangan tersebut seimbang
Jawaban:
Misalkan banyaknya kelereng tipe I adalah m sedangkan tipe II adalah n.
V1 = 4/3π(2)3 = 32/3π cm
V2 = 4/3π(4)3 = 256/3π cm
m x V1 = n x V2π
m x 32/3π = n x 256/3π
m = 8n
Sehingga, perbandingan banyak kelereng pada sisi kiri dengan sisi kanan agar seimbang adalah 8 : 1.
*) Disclaimer:
- Artikel ini hanya ditujukan kepada orang tua untuk memandu proses belajar anak.
- Sebelum melihat kunci jawaban, siswa harus terlebih dahulu menjawabnya sendiri, setelah itu gunakan artikel ini untuk mengoreksi hasil pekerjaan siswa.
(*)












![[FULL] Parpol 'Akali' Rakyat Pakai Diksi Nonaktifkan Kader dari Kursi DPR, Pakar: Masih Dapat Gaji](https://img.youtube.com/vi/8JfBdOqxz3E/mqdefault.jpg)




Isi komentar sepenuhnya adalah tanggung jawab pengguna dan diatur dalam UU ITE.